문제
세준이는 N*M크기로 직사각형에 수를 N*M개 써놓았다.
세준이는 이 직사각형을 겹치지 않는 3개의 작은 직사각형으로 나누려고 한다. 각각의 칸은 단 하나의 작은 직사각형에 포함되어야 하고, 각각의 작은 직사각형은 적어도 하나의 숫자를 포함해야 한다.
어떤 작은 직사각형의 합은 그 속에 있는 수의 합이다. 입력으로 주어진 직사각형을 3개의 작은 직사각형으로 나누었을 때, 각각의 작은 직사각형의 합의 곱을 최대로 하는 프로그램을 작성하시오.
입력
첫째 줄에 직사각형의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 직사각형에 들어가는 수가 가장 윗 줄부터 한 줄에 하나씩 M개의 수가 주어진다. N과 M은 100보다 작거나 같은 자연수이고, 직사각형엔 적어도 3개의 수가 있다. 또, 직사각형에 들어가는 수는 한 자리의 숫자이다.
출력
세 개의 작은 직사각형의 합의 곱의 최댓값을 출력한다.
풀이
먼저 이런 배열의 부분합을 구할 때는 누적합 알고리즘을 사용해야 한다. 참고
2차원 누적합, 부분합 구하기
누적합의 필요성 알고리즘 문제를 풀다보면 배열의 부분합을 빠르게 구해야 하는 경우가 있다. 필요할 때 마다 구하게 되면 구할 때 마다 //(O(N)//)의 시간 복잡도를 갖는다. 종만북 1번 문제 페스
eine.tistory.com
사각형을 나누는 방법은 다음과 같은 6가지 방법이 있다.
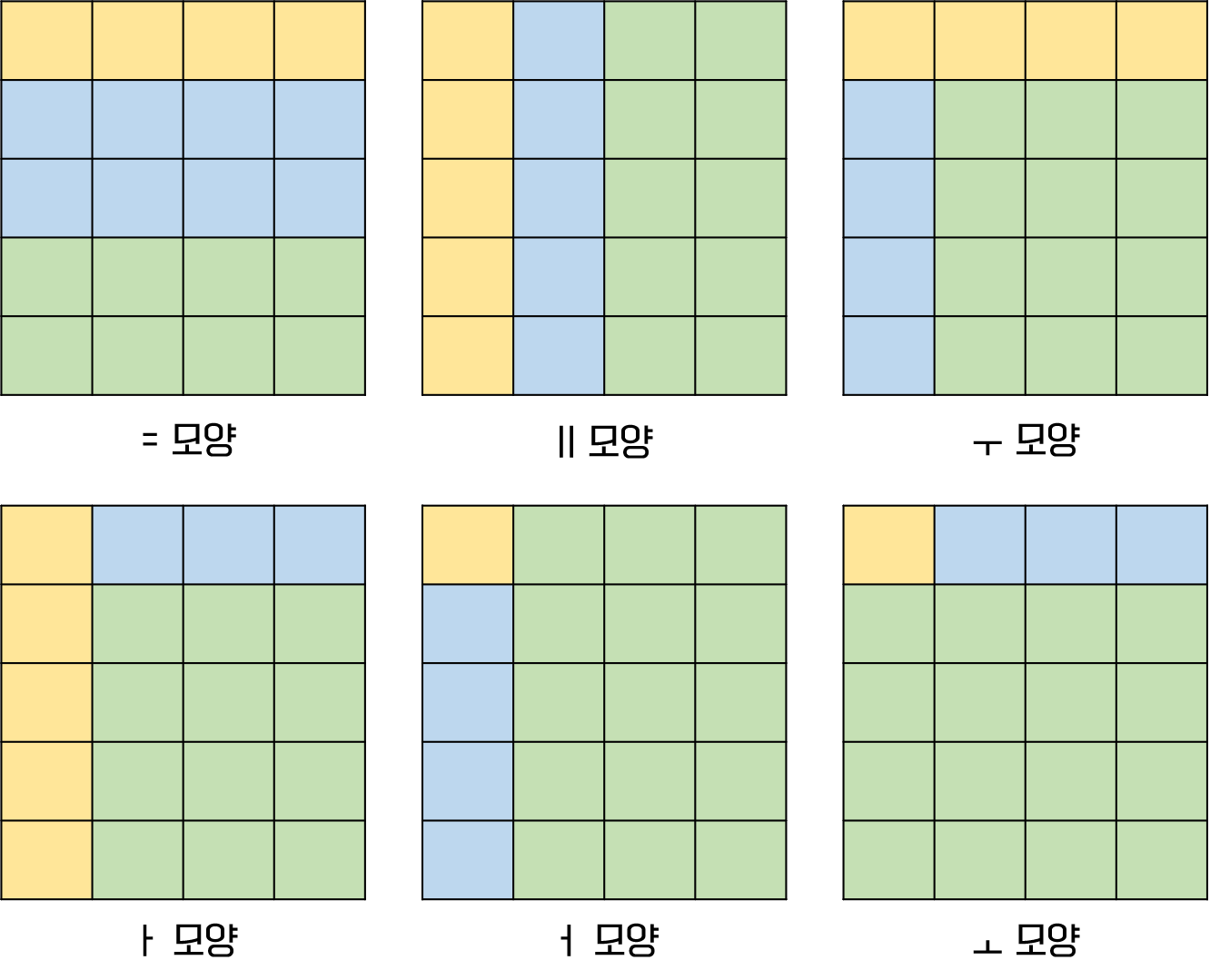
이렇게 나누는 것을 구현하면 된다...
또한 누적합이나 결과가 int형의 범위를 넘어갈 수 있으니 자료형에도 유의하자!
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static int[] divide;
static int[][] num;
static long[][] sum;
static long answer = 0;
static long[] temp;
public static long findSum(int x1, int y1, int x2, int y2) {
if (x1 == 0 && y1 == 0) {
return sum[y2][x2];
} else if (x1 == 0) {
return sum[y2][x2] - sum[y1 - 1][x2];
} else if (y1 == 0) {
return sum[y2][x2] - sum[y2][x1 - 1];
}
return sum[y2][x2] - sum[y2][x1 - 1] - sum[y1 - 1][x2] + sum[y1 - 1][x1 - 1];
}
public static void divideRow(int count, int index) { // 가로줄을 쭉 그었을때
if (count >= 2) {
temp[0] = findSum(0, 0, M - 1, divide[0] - 1);
temp[1] = findSum(0, divide[0], M - 1, divide[1] - 1);
temp[2] = findSum(0, divide[1], M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
return;
}
for (int i = index; i + 1 < N; i++) {
divide[count] = i + 1;
divideRow(count + 1, i + 1);
}
}
public static void divideCol(int count, int index) { // 세로줄을 쭉 그었을때
if (count >= 2) {
temp[0] = findSum(0, 0, divide[0] - 1, N - 1);
temp[1] = findSum(divide[0], 0, divide[1] - 1, N - 1);
temp[2] = findSum(divide[1], 0, M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
return;
}
for (int i = index; i + 1 < M; i++) {
divide[count] = i + 1;
divideCol(count + 1, i + 1);
}
}
public static void dividePoint() {
for (int i = 1; i <= N - 1; i++) {
for (int j = 1; j <= M - 1; j++) {
// ㅗ 모양
temp[0] = findSum(0, 0, j - 1, i - 1);
temp[1] = findSum(j, 0, M - 1, i - 1);
temp[2] = findSum(0, i, M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
// ㅜ 모양
temp[0] = findSum(0, 0, M - 1, i - 1);
temp[1] = findSum(0, i, j - 1, N - 1);
temp[2] = findSum(j, i, M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
// ㅏ 모양
temp[0] = findSum(0, 0, j - 1, N - 1);
temp[1] = findSum(j, 0, M - 1, i - 1);
temp[2] = findSum(j, i, M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
// ㅓ 모양
temp[0] = findSum(0, 0, j - 1, i - 1);
temp[1] = findSum(0, i, j - 1, N - 1);
temp[2] = findSum(j, 0, M - 1, N - 1);
answer = Math.max(answer, temp[0] * temp[1] * temp[2]);
}
}
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
num = new int[N][M];
sum = new long[N][M];
temp = new long[3];
for (int i = 0; i < N; i++) {
String s = br.readLine();
for (int j = 0; j < M; j++) {
num[i][j] = s.charAt(j) - '0';
if (i == 0 && j == 0) {
sum[0][0] = num[0][0];
} else if (i == 0) {
sum[0][j] = sum[0][j - 1] + num[i][j];
} else if (j == 0) {
sum[i][0] = sum[i - 1][0] + num[i][j];
}
}
}
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + num[i][j];
}
}
divide = new int[2];
divideRow(0, 0);
divideCol(0, 0);
dividePoint();
System.out.println(answer);
}
}'Old > 백준' 카테고리의 다른 글
| 백준 3109번 빵집 // JAVA (0) | 2021.02.18 |
|---|---|
| 백준 1009번 분산처리 // JAVA (0) | 2021.02.18 |
| 백준 17135번 캐슬 디펜스 // JAVA (0) | 2021.02.17 |
| 백준 18119번 단어 암기 // C++ (2) | 2020.12.06 |
| 백준 1167번 트리의 지름 // C++ (0) | 2020.09.03 |
